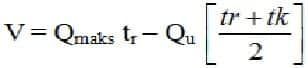Nr. 69. Overvannsdammer. Beregning av volum

Formål

Dette VA/Miljøblad beskriver metoder for beregning av nødvendig volum for å fordrøye overvann og dempe flomtopper. Dette kan skje med bl.a. åpne overvannsdammer eller lukkede tanker under jorden. I dette VA/Miljøbladet er betegnelsen magasin brukt, da både dammer og tanker kan brukes til samme formål.

Metodene er utdypet ved at et tenkt eksempel er beregnet med tre ulike metoder.

Begrensninger

Overvannsdammer skal ikke være et element i fellesavløpssystemer hvor spillvann kan komme inn. De metodene som beskrives forutsettes å gjelde dammer som primært skal anlegges for fordrøyning av overvannsflommer fra et gitt nedslagsfelt og ikke dammer som også er ment for rensing av overvann. I praksis gir overvannsdammer imidlertid både en fordrøyningseffekt og en renseeffekt. Metodene som beskrives er ment for manuell beregning. Det anbefales at man bruker regneark som gjør det enkelt å justere parametere og inngangsdata, gå ett steg tilbake i regneprosessen hvis man ser at en forutsetning var gal (iterasjon) og repetere ensartede regneprosedyrer. Det fins imidlertid kommersielle datamodeller som er spesielt utviklet for å beregne overvannsmagasiner. Metoder som ikke er for kompliserte, men likevel har akseptabel nøyaktighet er gitt i dette VA/miljøbladet. Den desidert største usikkerheten ligger i valg av avrenningskoeffisienten (φ) for avløpsfeltet. Denne kan ha en meget stor usikkerhet For eksempel kan et spenn fra φ = 0,2 til φ = 0,4 for et gitt felt være realistisk. Kraftig regn på frossen mark er et annet eksempel på forhold som kan gi 2-3 ganger mer avrenning enn det man dimensjonerte for.

Funksjonskrav

Ved bruk av de metodene som er beskrevet skal man få et volum i overvannsmagasinet som skal kunne beskytte nedstrøms avløpsnett, drensledninger, kulverter eller naturlige vassdrag mot for store vannføringer.

Løsninger

INNLEDNING

Fordrøyningsvolum bør beregnes så nøyaktig som mulig fordi overdimensjonering er dyrt og underdimensjonering kan gi skader på miljø, eiendom og infrastruktur. Utløpsarrangementet er helt avgjørende på om tømmingen skjer på en riktig måte. For stor utløpskapasitet gjør at volumet ikke utnyttes godt nok, og for liten utløpskapasitet gjør at magasinet overoppfylles og vann går i nødutløp. Det vises til VA/Miljøblad nr. 70 «Innløps- og utløpsarrangement ved overvannsdammer», og til VA/Miljøblad nr. 75 «Utforming av overvannsdammer» for dimensjonering av dammer for rensing av overvann.

HVA SKAL DET DIMENSJONERES FOR?

Norsk Vanns veiledning i overvannshåndtering (Lindholm et al. 2008) /4/ gir retningslinjer for minimum dimensjonerende gjentaksintervall. Dette varierer mellom 5 og 30 år for full kapasitetsutnyttelse, eller kritisk oppstuvningsnivå og med type område man arbeider med.

Ifølge Norsk Vanns veileder og Mays (2001 b) /7/ bør man vurdere å dimensjonere magasinets nødoverløp og etterfølgende åpne flomvei for en 100-årsflom. Praksis for valg av dimensjonerende gjentaksintervall er imidlertid sterkt avhengig av den lokale situasjon, f.eks. er et 2 års gjentaksintervall også brukt enkelte steder for overvannsdammer.

Det må også settes av plass til isdannelsen om vinteren i tillegg til det aktive utjevningsvolumet. Istykkelsen h (mm) kan beregnes etter Stefans ligning /5/.

h = a (D_f)^0,5 

a = en koeffisient som er gitt i tabellen under

D_f = summen av grad-dager under 0 ^oCelsius (10 minusgrader i to døgn gir D_f = 20)

Forhold	a
Teoretisk maksimum	34
Innsjø med mye vind og ikke noe snødekke	27
Innsjø med middels forhold med snødekke	17-24
Elv med middels forhold med snødekke	14-17
Beskyttet elv med rask strømning	7-14

TRE METODER MED ULIK DETALJERING OG KOMPLEKSISTET

Regnenvelopmetoden er basert på ideen med å beregne massebalansen i magasinet for kasseregn med forskjellige regnvarigheter, tatt fra IVF-kurver (regnintensiteteskurver). Den regnvarighet er dimensjonsgivende, hvor akkumulerte tilløpsmengder minus akkumulerte utløpsmengder er størst.

A. Enkel regnenvelopmetode med konstant utløp

Man antar et konstant utløp som er omtrent det man vil ha som en maksimalverdi tilpasset nedstrøms forhold. Butler og Davies /3/ foreslår valg av konstant utløp som for eksempel kan være bestemt av det nedslagsfeltet ga før det ble bebygd/utviklet. Dette kan være en verdi tilpasset arealet på nedslagsfeltet (f.eks 10 – 12 l/s ha) eller basert på kapasiteten til nedstrøms avløpsnett etter vassdrag. For å få et mest mulig representativt volum i beregningen, kan man velge utgående vannføring til f.eks. 70 % av den maksimalt tillatte verdien.

Når det konstante utløpet er bestemt er det bare å bruke den forenklede metoden for regnenvelopen direkte.

B. Aron og Kiblers metode

Hvis man ikke vil bruke konstant utløpsvannføring, kan man bruke Aron og Kiblers /2/ metode som forutsetter en lineært økende vannføring ut av bassenget, til maksimal fylling i bassenget er nådd. Etter dette antas en lineært synkende vannføring ut av bassenget.

C. Metode med utløpsmengde som funksjon av dybde i bassenget

For en bestemt regnvarighet beregner man en utløpsvannføring som er bestemt av vanndybden i magasinet. Denne vannføringen brukes i hele regnforløpet for det aktuelle regnet.

1. Når utløpet skal være bestemt av dybde i magasinet må man gjøre et valg for bunnarealet i m2 og for utløpshullets diameter før beregningene kan begynne. Man må da ha en viss formening om det omtrentlige volumet. Dette kan man få et inntrykk av ved å se på tilløpet av overvannsmengdene, som er uavhengig av bunnarealet og utløpsåpningen.
2. Anta areal i magasinet og maksimal dybde, samt en diameter i utløpsrøret som gir et passende maksimalt utløp.
3. For den foreløpige utformingen beregnes utløpsvannføringen og volumet i magasinet ved ulike vanndybder over utløpet.

Beregningsmetoder for de tre metodene

Beskrivelse

A. Regnenvelop med konstant utløp

1. Velg gjentaksintervall for dimensjoneringsregn, f.eks. 5 år.
2. Beregn tilløpsvolumer Vinn med forskjellige regnvarigheter. Når man plotter alle valgte Vinn som funksjon av regnvarigheten får man en kurve som kalles omhylningskurven (envelopen) for tilrenningen.
   V_inn = i_z,tr t_r A φ
   der i_z,tr er regnintensiteten for et kasseregn med gjentaksintervall z og varighet t_r, A er arealet av nedslagsfeltet og er lik avrenningskoeffisienten.
3. Velg et passende konstant utløp Q_ut. Man kan f.eks ta utgangspunkt i en maksimalt tillatt verdi som kan være bestemt av nedstrøms betingelser i avløpsnettet eller i et vassdrag. For å få en mest mulig gjennomsnittlig utløpsvannføring kan man f.eks velge 70 % av maksimalverdien. Beregn utløpsmengden Vut for forskjellige regnvarigheter:V_ut = Q_ut t_r
4. Beregn nødvendig volum for de forskjellige regnvarighetene t_r :V_fordrøyn = V_inn – V_ut
5. Bestem maksimalt nødvendig fordrøyningsvolum:

V_magasin er den største verdien av V_fordrøyn man finner. Dette gjøres ved å se på alle de regnvarigheter man har beregnet for.

B. Aron og Kiblers metode

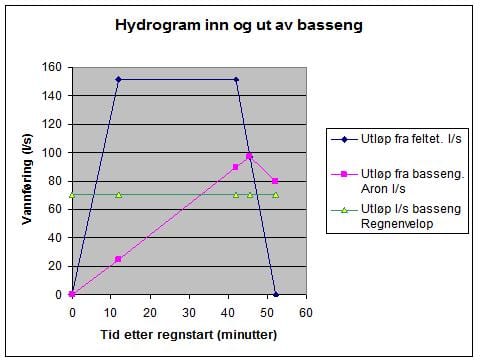
Aron og Kibler /2/ har beskrevet en metode som forutsetter at innløpet følger formen til et trapes. Videre at maksimumspunktet på utløpshydrogrammet ligger på den nedadgående delen av innløpshydrogrammet og at den tiltagende delen av utløpshydrogrammet kan tilnærmes til en rett linje som starter i origo. Se figur 1. Denne metoden forutsetter at man vet konsentrasjonstiden tk for feltet. I figur 1 er vist innløpshydrogrammet for et regn som varer i 40 minutter og hvor tk er 12 minutter. Skrålinjen er utløpet og den skjærer avtagende del av innløpshydrogrammet ved maksimalt utløp på 97, 4 l/s. Denne verdien er fremkommet fordi man har antatt at maksimal dybde over utløpsrøret, som har diameter 0,2 m, blir 1,0 m. Utløpshydrogrammet faller etter dette punktet og formen på denne delen av utløpskurven har ingen betydning for beregningen av maksimalt volum fordi maksimalt volum oppnås der utløpshydrogrammet skjærer innløpshydrogrammet. Volumet i magasinet er arealet mellom den blå innløpslinjen og den skrå røde utløpslinjen.

I figur 1 har man også lagt inn alternativet med konstant utløp på 70 l/s, som er den vannføringen det etterfølgenne eksempelet gir ved halvfylt magasin med dybde lik ca. 0,5 m over utløpsrøret. Arealet mellom innløpshydrogrammet og utløpshydrogrammene gir to alternativer for nødvendig magasinvolum og man ser at metoden til Aron og Kibler gir størst nødvendig volum.

Volumet i bassenget beregnes for hvert enkelt kasseregn man velger fra I-V-F kurven og er:

Her er V = nødvendig magasinvolum (m³), Q_maks = høyeste vannføring på innløpshydrogrammet (m³/s), t_r = regnvarighet (sekunder), Q_u = høyeste vannføring på utløpshydrogrammet (m³/s) og t_k = konsentrasjonstiden for nedslagsfeltet (sekunder).

Videre er:

Q_maks = φ A I

I figur 1 ser man at utløpsvannføringen fra feltet blir null etter 52 minutter som er summen av regnvarigheten og konsentrasjonstiden (t_r + t_k).
C. Regnenvelop med utløp som funksjon av dybde i bassenget

1. Velg gjentaksintervall for dimensjoneringsregn (f.eks. 5 år). Beregn tilløpsvolum V_inn for 5 års kasseregn med forskjellige regnvarigheter. Alle beregnede V_inn plottet i et diagram som funksjon av regnvarigheten kalles omhylningskurven (envelopen) for tilrenningen:V_inn = i_z,tr t_r A φder V_inn er tilrenningsvolumet fra feltet, φ er avrenningskoeffisienten for nedslagsfeltet, A er arealet til nedslagsfeltet (ha), t_r er regnvarigheten og i er regnintensiteten til kasseregnet fra I-V-F kurven (l/s ha).
2. Dersom man vil beregne med varierende utløp går man videre slik:
3. Velg utforming av magasinet, bl.a. overflate A_magasin og utløpstverrsnitt A_ut (f.eks. et dykket rør på bunnen av magasinet med en valgt diameter).Vannhøyden over røret kan anslåes ved at man antar at hele vannmengden renner inn fullt ut før utløp fra bassenget skjer, og man bruker halve vanndybden denne vannføringen inn gav for å beregne utløpsvannføringen.
4. Bestem utløpsvannføring Q_ut som funksjon av vannstand i magasinet. Qut er avhengig av vannstanden i magasinet hmagasin. Beregn utløpsmengde for forskjellige regnvarigheter:V_ut = Q_ut t_r
5. Beregn vannbalanse for forskjellige tilløpsvolum som en funksjon av regnvarighet t_r:
   V_fordrøyn  =  V_inn – V_ut
6. Bestem maksimalt nødvendig fordrøyningsvolum:

V_magasin  er den største verdien av V_fordrøyn man finner. Dette gjøres ved å se på alle de regnvarigheter man har beregnet.

Figur 1. Eksempel på et innløpshydrogram og utløps-hydrogram etter metoden til Aron og Kibler og metode med konstant utløp.

Begrensninger i regnenvelopmetodene

Dersom to eller flere regn kommer tett på hverandre kan dette føre til at magasinet ikke rekker å tømmes mellom hvert regn.

I følge Mays (2001 a) /6/ bør metodene ikke brukes på magasiner med et nedslagsfelt større enn ca. 12 ha. Dette fordi beregningene baseres seg på den rasjonelle formel som gjør en grov forenkling av avrenningsforløpet. I følge NS-EN 752 /9/ kan imidlertid den manuelle rasjonelle formel brukes opptil 200 ha. Vi anbefaler imidlertid at man ikke bruker den manuelle envelopmetoden for felt større enn 20 – 50 ha.

Dersom man vil ta hensyn til at vannføringen ut varierer med høyden over utløpet, må man anta et areal i bunnen av magasinet. Man kan anslå fyllingshøyden på flere måter, som for eksempel ved å anta at bassenget fylles først opp med all vannføring fra regnet før noe renner ut, og så bruke halvparten av denne høyden i hvert regn for å beregne vannføringen ut av åpningen i bassenget. Dette gir også delvis unøyaktige verdier spesielt ved meget lange regnvarigheter som gir store volumer og dermed høye fyllingsgrader. Det gir høye utløpsvannføringer og blir unøyaktig da vannføringene inn og ut av magasinet er mindre ved lange regn og utløpet starter lenge før magasinet er fylt av vannet inn.

Nedbørvolumet beregnes direkte med basis i ”kasseregnet” som tas fra intensitetsvarighets- frekvenskurven (I-V-F kurven). Dette fører til en undervurdering av den virkelige situasjonen da de utvalgte regn på I-V-F kurven har et forregn og etterregn som også bidrar til regnvolumet. Arnell /1/ fant at for et 30 minutter regn lå bare ca 50 % av totalt regnvolum i kasseregnet fra I-V-F kurven, mens et 60 minutters regn hadde ca 60 % og et 240 minutters regn ca. 80 % av totalt volum i kasseregnet. Dette undervurderer nødvendig volum. Feilen blir imidlertid langt lavere enn de prosentvise avvik som Arnell fant. Dette fordi volumet i etterregnet ikke bidrar særlig til maksimalt nødvendig volum, men mest til en økning i tømmetiden. Videre vil forregnet ha en lavere regnintensitet enn det kasseregnet har og feilen blir av denne grunnen også mindre enn det volumavviket tilsier.

Det forutsettes i den enkle regnenvelopmetoden at regnet faller direkte i magasinet, mens man i virkeligheten har en konsentrasjonstid som strekker vannføringen inn til magasinet ut i tid. Dette bidrar til å overvurdere nødvendig volum. I metoden til Aron et. al. gjøres imidlertid ikke denne feilen, da man tar hensyn til konsentrasjonstiden og dermed forsinkelsen i feltets avrenning.
Totalt sett kan man si at de unøyaktigheter som gjøres i noe grad utligner hverandre.

Tabell 1 gir en oppsummering av etterfølgende beregningseksempler med de metoder som er beskrevet. Tallene er påvirket av de antagelser som er gjort individuelt for de tre metodene.

Beregningsmetode	Beregnet maksimalt volum i m3
Regnenvelop med konstant utløp på 70 l/s	195
Regnenvelop med varierende utløp	177
Aron et. al	217

Tabell 1. Oppsummering av etterfølgende beregningseksempel.

Tabell 1 gir et inntrykk i variasjonen av beregningsresultater ved bruk av ulike metoder.

BEREGNINGSEKSEMPLER

VANLIG REGNENVELOPMETODE MED KONSTANT UTLØP

Vi antar et avløpsfelt på 20 ha med = 0,3 og konsentrasjonstid på 12 minutter.

Det antas at magasinet ligger i et område med lavt skadepotensiale og Norsk Vanns veileder sier da at man bør velge en regnkurve med 5 års gjentaksintervall.

Regnintensiteten i (l/s ha) antas å følge følgende formel:

i = 244 / (t + 1,5)^0.61

der t = regnvarighet i minutter.

Det antas at man ønsker et maksimalt utløp på ca. 100 l/s. Den virkelige gjennomsnittlige utløpsmengden vil ligge lavere enn den maksimale. For å få en mest mulig korrekt volumberegning antas det at gjennomsnittlig utløp er 70 % av maksimalt utløp. Det antas derfor et beregningsmessig utløp på 70 l/s.

Når magasinet skal bygges må man ha en utløpsanordning som gir korrekt strupning. Se VA/Miljøblad nr. 70.

For å vise en detaljert beregning med denne metoden er tallene for en regnvarighet på 15 minutter vist.

Regnintensitet for t_r = 15 minutter:
i = 244/(15 +1,5)0,61 = 44,13 l/s ha

Innløp = 0,3 ∙ 20 ∙ 44,13 ∙ 15 ∙ 60 = 238 302 l = 238,3 m³

Utløp = 70 ∙ 15 ∙ 60 = 63 000 l = 63 m³

Nødvendig magasin for et 15 minutters regn = 238 – 63 = 175 m³

Regnvarighet	Innløp fra feltet	Utløp fra basseng	Maks volum
t = [min]	[m3]	[m3]	[m3]
15	238	63	175
20	270	84	186
30	321	126	195
40	362	168	194
50	397	210	187
60	427	252	195
120	564	504	60

Tabell 2. Regnenvelop med konstant utløp fra magasinet.

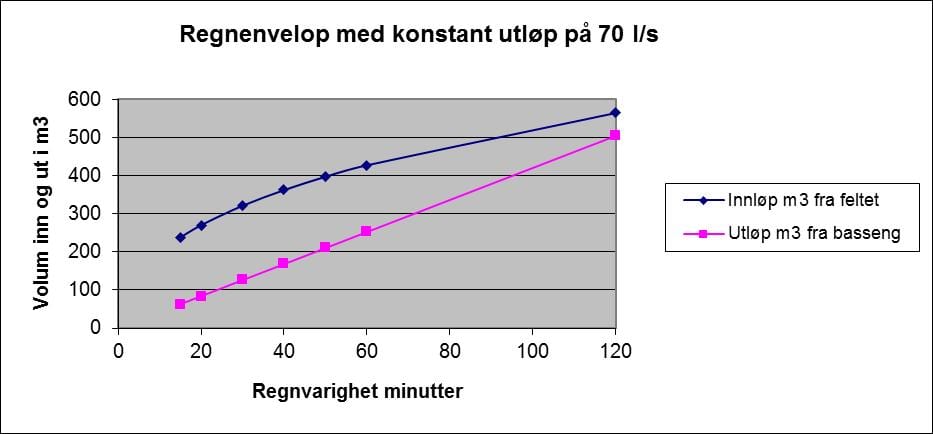
Man ser av tabell 2 at maksimalt nødvendig volum skjer for et 30 minutters regn og blir 195 m3. Figur 2 viser tabell 2 i diagramform. Maksimal vertikal avstand mellom de to kurvene i figur 2 representerer nødvendig volum.

Figur 2. Regnenvelop med konstant utløp på 70 l/s.

VOLUMBEREGNING ETTER ARON OG KIBLERS METODE

Det antas de samme basisforhold som i det første eksemplet ovenfor.

Det er antatt et maksimalt utløp på 97,4 l/s. Dette er et tall som kommer fra det tredje (og siste) eksempelet i dette VA/Miljøbladet. Det er ikke ment å være et gjennomsnittlig tall, men det høyeste utløpet, noe som skjer når vannet står 1 meter over utløpsrøret i det tredje eksempelet. Resultatet av denne beregningen for regnvarighet på 40 minutter er fremstilt i figur 1 og som man ser av tabell 3 får man et maksimalt volum på ca. 217 m3 ved en regnvarighet på 60 minutter.

For å igjen vise en detaljert beregning med Aron og Kiblers metode er tallene for en regnvarighet på 15 minutter vist.

Feltets avrenningskoeffisient = 0,3 og feltets areal = 20 ha

Regnintensitet for t_r = 15 minutter:
i = 244/(15 + 1,5)^0,61 = 44,13 l/s ha

Q_maksinnløp = 0,3 ∙ 20 ∙ 44,13 = ca. 265 l/s

Utregning:
V = 265 ∙ 15 ∙ 60 – 97,4 ∙ ((15 + 12) ∙ 60)/2)
= 159.408 l = ca. 159,4 m³

Regnvarighet [min]	Regnintensitet [l/s ha]	Qmaksinn [l/s]	Volum [m3]
12	49,88	299	145,3
15	44,13	265	159,4
20	37,55	225	176,9
30	29,75	178	198,5
40	25,14	151	210,1
50	22,04	132	215,5
60	19,78	119	216,8
70	18,04	108	215,0
80	16,66	100	210,9

Tabell 3. Volumberegning etter Aron og Kiblers metode.

METODE MED UTLØP SOM FUNKSJON AV VANNDYBDEN

Det antas de samme basisforhold som i eksemplene ovenfor.

Utløpsrørets diameter i bunnen på magasinet velges til D = 0,2 meter.

Det antas et dykket fritt utløp og vannføring ut av røret blir da:

Q_ut = 0,7 ∙ 3,14 ∙ D²/4 ∙ (2gh)^0.5

Vanndybden i magasinet over røret er h meter.

For å anslå et midlere konstant utløp kan man beregne tilløpsvolumene først. Man kan da danne seg et inntrykk av hva nødvendig magasinvolum kan bli.

Det anslåes her at det kan bli ca 210 m³. Det er nødvendig å anta et areal i bunnen av magasinet.

Det velges da et magasin med 210 m² bunnareal og en antatt dybde på ca. 1 meter. I henhold til Sjöberg og Mårtensen /10/ velger man den konstante utløpsvannføringen til vannføringen ved halvfylt magasin, d.v.s. ved 0,5 meter.

Q_ut gjennom røret blir ved en vanndybde på 0,5 m ca. 70 l/s.

Man kan tenke seg flere måter å få frem høyder over utløpsrøret ved de forskjellige regnvarighetene (dette bestemmer utløpsvannføringen). I det følgende brukes følgende metode. Man later som utløpsrøret er stengt inntil hele regnets vannmengde fra feltet har rent inn i magasinet. Man beregner hvilken dybde h i magasinet (med areal på 210 m²) man da får. Dette er en for stor dybde da jo utløpet starter lenge før alt har rent inn. Derfor brukes i dette eksempelet en høyde lik halve dybden h for det enkelte regn.

For alle kasseregn beregnes totalt tilløp, høyde h/2 og vannføring fra utløpsrøret som dette gir. Se tabell 4.

For å vise beregningene i detalj gjennomføres beregningene for en varighet på 20 minutter.

Regnintensiteten blir = i₂₀ = 244/ (20 + 1,5)0,61 = 37,55 l/s ha

Overvann inn fra feltet: Vannmengde_inn = (0,3 ∙ 20 ∙ 37,55 ∙ 20 ∙ 60)/1000 = 270,4 m³

Denne mengden fyller opp bassenget med 270,4 / 210 = 1,29 m

Halve denne oppfyllingshøyden = 1,29/2 = 0,64 m

Utløpsvannføringen fra røret blir Q_ut = 0,7 ∙ 3,14 ∙ 0,22/4 ∙ (2 ∙ 9,81 ∙ 0,64)0,5 = 0,07789 m³/s

Vannmengde_ut = 0,0779 ∙ 20 ∙ 60 = 93,5 m³

Nødvendig magasinvolum for et 20 minutters regn blir = 270,4 – 93,5 = 176,9 m³

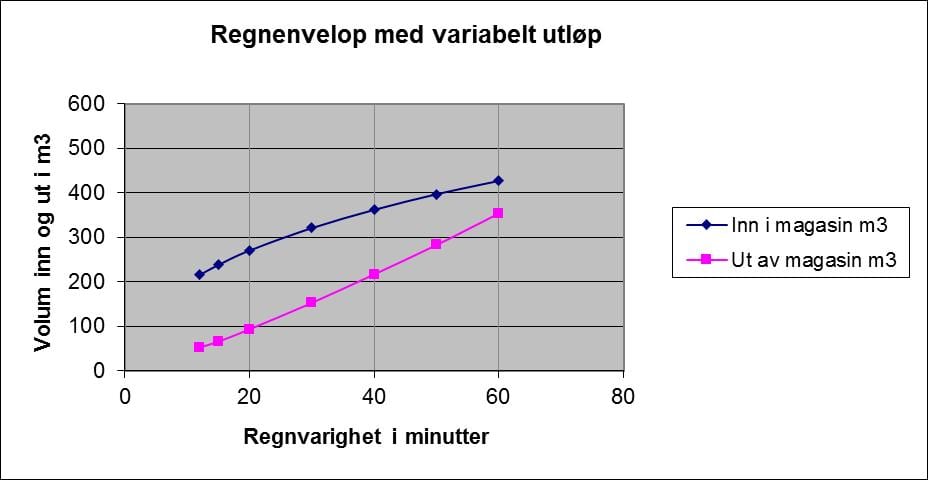
Resultatene fra tabell 4 er vist i figur 3. Maksimalt nødvendig volum blir ca. 177 m³ som er største vertikal avstand mellom de to kurvene i figur 3, d.v.s Volum_inn – Volum_ut.

Regn-varighet	Regn-intensitet	Overvann	Innløp volum	Qmaks inn	Halve h i magasinet	Qut	Utløp volum	Nødv. magasin
t [min]	i [l/s ha]	[l/ha]	fra feltet [m3]	[l/s]	[m]	[m3/s]	[m3]	[m3]
12	49,88	10773	215,5	299	0,51	0,0735	52,9	163
15	44,13	11915	238,3	265	0,57	0,0735	66,2	172
20	37,55	13518	270,4	225	0,64	0,078	93,6	177
30	29,75	16063	321,3	178	0,76	0,085	153,0	168
40	25,14	18101	362,0	151	0,86	0,0903	216,7	145
50	22,04	19835	396,7	132	0,94	0,0944	283,2	113
60	19,78	21360	427,2	119	1,02	0,0983	353,9	73

Tabell 4. Regnenvelop med varierende utløp fra regn til regn.

 

Figur 3. Regnenvelop med utløpsmengde som funksjon av vanndybden i magasinet.

 

 

 

Henvisninger:		Utarbeidet:	november 2006	Oddvar G. Lindholm
/1/	Arnell, V. 1982. ”Rainfall data for the design of sewer pipe systems”. Chalmers Tekniska Högskola. Report series A:8. Göteborg.	Revidert:	juni 2015	Oddvar G. Lindholm
/2/	Aron, G. and Kibler, D.F. 1990. ”Pond sizing for Rational Formula Hydrographs” Water Resources Bulletin AWRA, vol. 26, no.2, pp 255-258.	/7/	Mays, L.W. 2001 b. “Stormwater Collection Systems Design Handbook” McGraw-Hill.
/3/	Butler, D. and Davies J. W. 2000. “Urban drainage”. E & FN SPON.	/8/	Metropolitan Council/Barr Engineering Co.  “Minnesota Urban Small Sites BMP      Manual”.
/4/	Lindholm, O., Endresen, S. Thorolfsson, S., Sægrov, S. og Jakobsen, G. og Aaby, L. 2008. ”Veiledning i klimatilpasset overvannshåndtering”. NORSK VANN-rapport 162 – 2008.	/9/	Norsk standard NS-EN 752-2. 1997 ”Utvendig stikklednings- og hovedledningssystemer”.
/5/	Marsalek, P.M., Watt, W.E., Marsalek, J. and Anderson, B.C. 2000. ”Winter Flow Dynamics of an On-Stream Stormwater Management Pond”. Water Quality Research Journal of Canada, 35 (3):505-523. Burlington, Ontario.	/10/	Sjöberg, A. og Mårtensson, N. 1982. ”Regnenveloppmetoden”. Chalmers Tekniska Högskola. Meddelande nr. 64. Göteborg.
/6/	Mays, L. W. 2001 a. ”Water Resources Engineering”. John Wiley & sons.	/11/	Walker, W.W. 1987. ” Design Calculations for Wet Detention Ponds”. Prepared for the St. Paul Water Utility and Vadnais Lake Area Water Management Association. St. Paul.