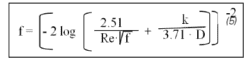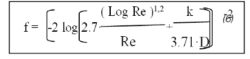Nr. 101. Hydraulikk tilpasset VA-anlegg

Formål

Hydraulikk inngår på en eller annen måte ved gjennomføring og drift av de fleste VA anlegg, og det er derfor viktig med kunnskap knyttet til ”praktisk” hydraulikk.

Dette VA/Miljø-bladet gir informasjon om grunnlaget for dimensjonering ved transport av vann i trykk- og selvfallsledninger, samt i kanaler.

Det gis også informasjon om beregning av mengder i overløp, tap ved transport gjennom rørdeler og armatur, mm.

Begrensninger

Det gis ikke detaljert informasjon knyttet til:

• Grunnleggende hydrauliske formler
• Ulike formler for singulærtap. (enkelttap)

Funksjonskrav

Hydrauliske beregninger skal bidra til VA-anlegg med riktige dimensjoner, og sørge for at driftstekniske funksjoner ivaretas.

Løsninger

Det skilles mellom to typer strømninger:

• Laminær strømning
• Turbulent strømning

Allerede i 1883 fant Reynolds ut at overgangen fra laminær til turbulent strømning skjedde ved en bestemt kritisk hastighet, og innførte det dimensjonsløse Reynolds tall (R_e).

R_e = (v • d )/ γ (1)

v = vannhastighet (m/sek)

d = hydraulisk diameter (m)

γ = kinematisk viskositet (m²/sek)

d = 4 • A/O (2)

A = rørets eller kanalens våte areal i m²

O = våt omkrets i m

Ved fullt sirkulært rør er hydraulisk diameter (d) lik innvendig rørdiameter (D)

d = 4 (π • D² /4)/ ( π x D) = D (3)

Kinematisk viskositet i forhold til vanntemperatur vises i tabell 1.

Vanntemperatur °C	Kinematisk viskositet m2 /sek
1	1.7321• 10-6
5	1.5188• 10-6
10	1.3107• 10-6
15	1.1457• 10-6
20	1.0105• 10-6

Tabell 1. Kinematisk viskositet

HASTIGHETER VED LAMINÆR OG TURBULENT STRØMNING

R_e < 2300 gir laminær strømning.

R_e > 4000 gir turbulent strømning

Ved R_e mellom 2300 og 4000 kan begge typer strømning forekomme.

Eksempel på vannhatigheter ved laminær- og overgang til turbulent strømning, når vann-temperaturen er 10 °C, vises i tabell 2.

Innvendig rørdim mm	Laminær str.Hastighet under m/sek	Turbulent str. Hastighet over m/sek
50	0.06	0.10
100	0.03	0.05
200	0.02	0.03

Tabell 2.Vannhastigheter ved laminær og turbulent strømning.

Etterfølgende beregninger baseres derfor på formler knyttet til turbulente vannstrømmer.

BEREGNING AV TRYKKTAP I SIRKULÆRE RØR.

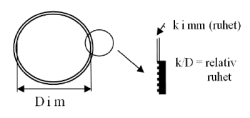
Tapet vil være avhengig av flere forhold, blant annet innvendig ruhet k. (illustrert i figur 1 )

Figur 1 Innvendig ruhet (ujevnheter)

Tapet beregnes med Darcy- Weisbachs formel:

h_f = f • ((L/D) • (v² /2•g)) (4)

h_f = tap i meter vannsøyle

L = ledningslengden i meter

D = ledningsdiameter i m

v = vannhastigheten i m/sek

g = tyngdens akselerasjon (9.81 m/sek² )

f = tapskoeffisienten som er dimensjonsløs

f er avhengig av:

– Relativ ruhet (k/D)

– Vanntemperatur. (Kinematisk viskositet)

– Reynolds tall

Når ovennevnte er kjent kan f beregnes.

Formler for beregning av tapskoeffisienten f

En felles formel, som for praktisk bruk dekker alle situasjoner, ble utviklet av Prandtl, Colebrook og White: (formel 5)

Formelen må imidlertid løses med iterasjon. Det er også utviklet en formel (6) som gir tilnærmet riktig løsning, uten bruk av iterasjon:

Tapskoeffisienter til praktisk bruk.

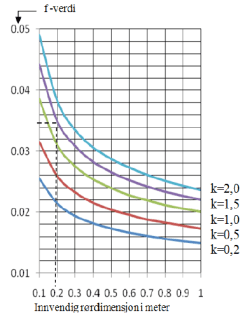
Tapskoeffisienter i forhold til k-verdi vises i tabell 3. og figur 2 (vanntemperatur 10 °C).

Rørdim.mm	k-verdi
	0.5	1.0	1.5	2.0
100	0.03157	0.03868	0.04429	0.04914
200	0.02586	0.03099	0.03495	0.03830
300	0.02321	0.02751	0.03079	0.03354
400	0.02157	0.02538	0.02827	0.03068
500	0.02041	0.02390	0.02653	0.02871
600	0.01953	0.02278	0.02522	0.02724
700	0.01883	0.02190	0.02418	0.02608
800	0.01826	0.02117	0.02334	0.02513
900	0.01777	0.02056	0.02263	0.02434
1000	0.01735	0.02004	0.02203	0.02366

Tabell 3. Tapskoeffisienter i forhold til k-verdier.

Variasjoner i vanntemperatur vil i liten grad påvirke trykktapet (ca.0.8 % ved endring fra 5°C – 20°C).

Valg av k-verdi for VA ledninger:

For nye rør vil k-verdien variere i forhold til rørmateriale og innvendig belegg.Vanlig k-verdi, etter noe tids bruk er ca. 0,5 – 1.5 mm (størst for avløpsledninger pga. begroing) Det anbefales målinger. (se avsnitt 4.2.3)

Figur 2 f-verdi i forhold til k-verdi

Når f er kjent kan rørtapet beregnes med Darcy – Weisbachs formel. (formel 4)

Eksempel på beregning av trykktap:

• Innvendig rørdiam.(D) 0.4 m (Ø 400 mm)
• k- verdi 0.5 mm
• Vannmengde ( q ) 0.15 m³/sek
• Ledningslengde 1200 m
• Tygdens akselerasjon 9.81 m/sek²

f verdien tas ut av tabell 3, og blir for rørdiameter 400 mm med k-verdi 0,5 = 0.02157.

Vannhastigheten (v) =vannmengden /vått areal v=q / ((π•D²)/4)=0,150 / ((3,14•0,4²)/ 4)=1,194 m/s.

Nå er alle nødvendige verdier kjent, og tapet h_f kan beregnes etter formel (4):

h_f = 0,02157 •((1200/0,4) •1,194² /(2•9,81)) = 4,70 m

Beregning av f verdi for å bestemme k-verdi.

Det vil ofte være av interesse å klarlegge k-verdien for eksisterende ledninger.

Når trykktap (h_f) og mengden (q) er registrert kan f- beregnes, og k-verdien tas ut av figur 2. Formel 4 kan da omskrives i forhold til f:

f = (12,1026 • h_f • D⁵ ) / ( L • q² ) (7)

Eksempel:

• Ledningsdiameter (D)= 0,2 m
• Ledningslengde (L)= 800 m
• Registrert mengde: (q)= (0,040 m³/sek)
• Registrert tap: (h_f)= 11,5 m

f =(12,1026 •11,5 • 0,2⁵) /(800 • 0,040²) = 0,0348

k – verdien kan nå tas ut av figur 2, og følgende gjøres:

1. Gå inn på verdien for f ca. 0,035 på den vertikale aksen, og gå fram til skjæring med den vertikale linja for rørdimensjon 0,2 m.
2. Les av tilnærmet verdi for k, som er ca. 1,5.

SINGULÆRTAP

Når vannstrømmen påvirkes av endringer, slik at det dannes virvler, fås tap som benevnes singulærtap.

Formel for singulærtap (h_s):

h_s = K • (v² / (2 • g)) (8)

K = tapskoeffisient

v²/2g er et viktig begrep i hydraulikken, og benevnes ”hastighetshøyde” (energien som trengs for å sette vannet i bevegelse). VA hydrauliske tapsberegninger settes sammen av:

• Tap i rette rørstrekninger, pluss summen av singulærtap

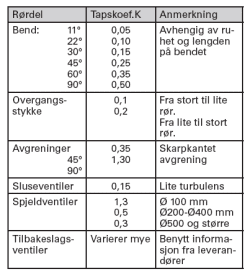
Eksempel på tapskoeffisienter for beregning av singulærtap vises i tabell 4. (vil variere).

Tabell 4. Eksempel på tapskoeffisienter ved singulærtap

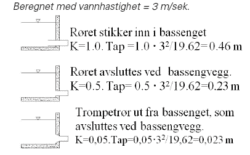
Eksempel på singulærtap ved tapping fra basseng

Etablering og utforming av utløpsstusser har stor betydning, slik det vises i figur 3.

 

Figur 3. Eksempel på singulærtap.

TRYKK – OG ENERGILINJE

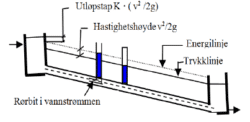
I figur 4 illustreres trykk- og energilinje ved tapping fra og til basseng.

Figur 4. Trykk- og energilinje.

Hele hastighetshøyden tapes når vannet ledes inn i bassenget.

Ved trykkmåling er det vannivået opp til trykk-linjen som registreres. (illustrert på skissen)

Hvis et rør føres inn i senter av vannstrømmen vil vannivået nå opp til energilinjen.

Hastighetshøyden er relativt liten ved normale hastigheter:

• ca. 5 cm ved hastighet 1 m/sek
• ca. 20 cm ved hastighet 2 m/sek

SELVFALLSLEDNINGER

Ved selvfallsledninger vil fyllingshøyden variere i forhold til transportert mengde.

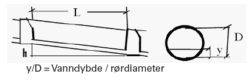
Utgangspunktet for beregninger er forholdet mellom vanndybde ved delfylling (y) og innvendig rørdiameter (D), dvs.( y/D.), slik det vises i figur 5.

Figur 5. Selvfallsledning med delfylling.

Brettings formel (9) benyttes vanligvis for beregning ved delfylte ledninger. Det vanlige er å benytte liten q for mengde , men her benyttes Q.

Q/Q_f=0,46 –0,5•COS(π•y/D)–0,04•COS(2•π•y/D) (9)

π = radianer = 180 °

y og D angis i meter

Q_f = vannmengde ved fullt rør m³/sek

Q = vannmengde ved delfylling m³/sek

Når Q/Q_f er klarlagt kan følgende bestemmes med Brettings formel:

• A/A_f = areal defylling /areal fullt rør
• v/v_f = hastighet delfylling /hastighet fullt rør
• R/R_f = hydraulisk radius delfylling/hydraulisk radius fullt rør

Hydraulisk radius = vått areal / våt omkrets, som for fullt rør blir ((π/4) •D² ) /(π • D) =D/4 m.

I tabell 5 vises relative verdier for Q/Q_f ,A/A_f , v/v_f og R/R_f i forhold til y/D.

y/D	Q/Qf	A/Af	v/vf	R/Rf
0,1	0,01683	0,052	0,3232	0,254
0,2	0,06785	0,142	0,4767	0,482
0,3	0,15375	0,252	0,6092	0,684
0,4	0,27313	0,374	0,7311	0,857
0,5	0,42000	0,500	0,8400	1,000
0,6	0,58215	0,626	0,9293	1,111
0,7	0,74153	0,748	0,9918	1,185
0,8	0,87687	0,858	1,0224	1,217
0,9	0,96789	0,948	1,0211	1,192
1,0	1,00000	1,000	1,0000	1,000

Tabell 5.

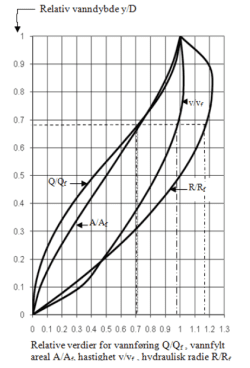
For praktisk bruk er det hensiktsmessig å overføre verdiene til et delfyllingsdiagram, slik det vises i figur 6.

Eksempel på bruk av delfyllingsdiagrammet

Gitt:

• Ledningsdiameter (D) = 0,5 m
• Fall (h/L) 5% = 0,005 m/m
• k-verdi (ruhet) = 1,0 mm
• Tapskoeffisient (f) = 0,0239
• Dim.vannmengde (Q) = 0,200 m³/sek

Følgende gjøres:

1. Beregn kapasiteten for fullt rør med formel (10).

Omskrevet formel 4.

Q_f = 3,4789 • D² • ( h • (D / f))^0,5 (10)

Når verdiene i eksemplet settes inn fås:

Q_f = 3,4789 • 0,5² • (0,005 • (0,5/ 0,0239))^0,5 = 0,281 m³/sek

 

Figur 6: Delfyllingsdiagram etter Brettings formel (fra tabell 5.)

2. Nå kan relativ verdi for Q / Qf beregnes, og blir 0,200 / 0,281 = ca. 0,71.

3. Gå inn med 0,71på aksen for relative verdier i delfyllingsdiagrammet, og fortsett opp til skjæring med kurven for Q/Q_f. Herfra gås horisontalt til aksen for relativ vanndybde (y/D), som blir ca. 0,68.

4.Nå kan vanndypet y beregnes, og blir for rør med diameter 0,5 m = 0,68 • 0,5 = ca.0,34 m.

5.Relativ vanndybde (0,68), sammen med data for fylte rør, kan nå benyttes for å finne verdier for delfylling. Beregning av data for fylte rør:

A_f = (π /4) • 0,5² = 0,196 m²

v_f = Q_f /A_f = 0,281/0,196 = 1,431 m/sek

R_f = D/4 = 0,5 / 4 = 0,125 m

6. Fra relativ vanndybde y/D = 0,68 gås horisontalt fram til kurvene for v/v_f , A/A_f og R/R_f.

7. Fra skjæringspunkter med respektive kurver gås ned til linjen for relative verdier, som gir grunnlaget for beregning av delfylte verdier:

A/A_f = 0,72. A_f = 0,196 og

A = 0,72 • 0,196 = 0,141m²

v/v_f = 0,98. v_f = 1,431 og

v = 0,98 • 1,431 =1,40 m/sek

R/R_f = 1,17 R_f = 0,125 og

R = 1,17 • 0,125 = 0,146m

Selvrensningshastighet

For selvrensning: Se VA/Miljø-blad nr. 79.

TRANSPORT I KANALER

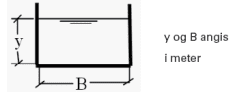
Det er ulike utforminger av kanaler, for eksempel støpte og gravde slik det illustreres i figurene 7 og 8.

Figur 7 Støpt betongkanal

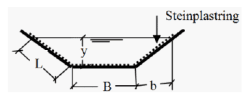
Figur 8 Gravd kanal med steinplastring

Den mest hensiktsmessige empiriske formelen, for kanaler og åpne vannveier, er utviklet av Gauckler, Manning og Strickler. Benevnes vanligvis Mannings formel (12).

v = M • R^2/3 • I^1/2 (11)

v = vannhastighet i m/sek = Q/A

M = Mannings tall

R = hydraulisk radius m (vått areal / våt omkrets)

I = bunnens fall m/m ( 2‰ fall = 0.002 m/m)

Q = vannmengde i m³ /sek

A = vått areal i m²

Ruhetsfaktoren k i forhold til Mannings tall M beregnes med formel 12.

M = 26 / k^1/6 (12)

k angis i meter.

Gjelder i følgende intervall 4.7 < R/k < 300

k = 0.0015m gir M = 26/0.0015^1/6 = ca 77

Mannings tall

Som nevnt er Mannings tall avhengig av ruheten, og vil variere mye i forhold til kanaler som bygges i betong eller stål, og de som graves i ulike masser med erosjonssikring, eller sprenges i fjell.

Noen eksempler vises i tabell 6:

Type kanal	Ruhet k m	Mannings tall M
Gravd i jord, og erosjons- sikret med steinmateriale	0,17- 0.080	35 – 40
Stål	0.001	82
Betong	0.002	73

Tabell 6: Eksempel på ruhet og Mannings tall

Eksempel på beregning av vannføring i betongkanal (figur 7)

Forutsetning:

• Rektangulær form
• Bunnbredde 0,75 m
• Vanndyp 0,50 m
• Fall 2,0 ‰ = 0,002 m/m
• Mannings tall 73

Hydr.radius =(0,75 • 0,5) / (0,75+(2 • 0,5))=0,2143 m

Beregning:

v = M • R^2/3 • I^1/2 =73 • 0.2143^2/3• 0.002^0.5 = 1.17m/sek

Q = A • v = (0.75 • 0.5) • 1.17 = 0.439 m³/sek

Vanndyp meter	Hastighet m/sek	Vannføring m3/sek
0,1	0,60	0,045
0,3	0,98	0,222
0,5	1,17	0,439
0,7	1,28	0,670
0,9	1,35	0,908

Tabell 7: Eksempel på hastighet og vannføring i ovennevnte kanal(i forhold til vanndyp).

Eksempel på vannføring i gravd steinplastret kanal (figur 8)

Forutsetning:

• Trapesformet med skråning 1:1.5
• Skråningsvinkel ca. 33,7 °
• Bunnbredde (B) 3,00 m
• Skråningsbredde (b) 2.25 m
• Skråningslengde (L) 2,70 m
• Vanndyp (y) 1,50 m
• Vannareal (3+2.25) • 1,5 = 7,875 m²
• Fall 2,0 ‰ = 0,002 m/m
• Mannings tall 37

Hydr.radius ((3,0+2,25)•1,5)/(3,0+2 •2,70) = 0,937 m

Beregning:

v=M•R^2/3 •I^1/2 = 37 • 0,937^2/3 • 0,002 ^0,5 =1.584 m/sek

Q = A • v = 7,875 • 1,584 = ca.12,47 m³/sek

Vanndyp meter	Hastighet m/sek	Vannføring m3/sek
0,1	0,34	0,11
0,3	0,66	0,69
0,5	0,88	1,66
1,0	1,28	5,77
1,5	1,58	12,47

Tabel 8: Eksempel på hastighet og vannføring i ovennevnte kanal(i forhold til vanndyp)

OVERLØP

I dette databladet er det bare beregning av vannmengder i rektangeloverløp som gjennomgås.

Rektangeloverløp

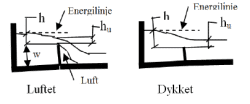
Det skilles mellom luftet og dykket overløp, slik det illustreres i figur 9.

Figur 9: Prinsipp av luftet og dykket overløp

Luftet overløp

Generell formel (13) for luftet overløp (luft under overløpsstrålen):

Q = (2/3) • µ • b • (2g)^0,5 • h^1,5 (13)

Q = vannmengde i m³/sek

µ = koeffisient avhengig av overløpsformen

b = overløpets bredde i m

g = tyngdens akselerasjon 9,81 m/sek²

h = høyde over overløpskanten i m (måles i en avstand tilsvarende ca 4 -5 ganger h_u)

Det er utviklet ulike formler for å bestemme overløpskoeffisienten (µ), der også betydningen av vanndypet foran overløpet inngår (w). For skarpkantet overløp og h/w < 2 blir µ ca. 0,60 + 0,08 • (h/w).

Eksempel på µ ved 0,5 m dyp foran overløpet:

• Overløpshøyde h 0,1 m gir µ = ca 0,62
• Overløpshøyde h 0,3 m gir µ = ca 0,65
• Overløpshøyde h 0,5 m gir µ = ca 0,68

Det er relativt liten variasjon i µ innenfor normale overløpshøyder, og for praktisk bruk foreslås å benytte 0,65.

Forenklet formel blir da som (14):

Q = 1,92 • b • h^1,5 (14)

Q = vannmengden i m³/sek

Dykket overløp

Formelen er den samme, bortsett fra en reduksjonsfaktor (c) som er avhengig av forholdet h_u/h. (se tabell 9)

Forenklet formel (15) blir da:

Q = 1,92 • b • c • h^1,5 (15)

hu / h	c
1,00	0
0,90	0,62
0,80	0,78
0,70	0,86
0,60	0,91

Tabel 9: Reduksjonsfaktor i forhold til h_u / h

Eksempel på beregning av mengde:

• Nivå før overløp (h) = 0,30 m
• Nivå etter overløp (h_u) = 0,20 m
• Overløpsbredde (b) = 2,00 m
• h_u/h = 0,20/0,30 = 0,67

Reduksjonsfaktor(c) = ca 0,89 (Fra tabell 9)

Q = 1,92 • b • c • h^1,5 =1,92 • 2,0 • 0,89 • 0,3^1,5 =

0,562 m³/sek

BRUK AV REGNEARK

For praktiske hydrauliske oppgaver er det hensiktsmessig å benytte regneark.

Formlene i dette miljøbladet kan benyttes ved etablering av regnearkene.

Henvisninger:		Utarbeidet:	mars 2012	Roar Finsrud
		Revidert:	nov 2013